The combination of redox and balancing chemical equations is enough to strike fear into the heart of any chemistry student. Read on to learn how to master this essential skill…

In my last blog, I covered seven rules you can use to balance chemical equations, which make up the ‘balancing by inspection’ method. This time, we’re looking at redox balancing.

Note this technique as a way of balancing equations is not for GCSE chemistry students, though there is nothing to stop you seeing how it works.

Redox reactions and electrons

Remember OILRIG – Oxidation is Loss, Reduction is Gain? In a chemical reaction, oxidation and reduction always happen together. Electrons lost from an element during oxidation must be gained by another element when it gets reduced. Otherwise, you’d have homeless electrons floating around…

This is another application of the law of Conservation of Matter. Since we’re dealing with transfer of electrons, which are a form of matter, we can’t create or destroy them in a chemical reaction. From this, we can conclude something very important about redox processes:

The number of electrons lost in the oxidation reaction = the number of electrons gained in the reduction reaction

How is that useful? It’s useful because knowing how many electrons were transferred helps us work out the balancing numbers, which is what we’re after if we want to balance a chemical equation.

Steps for balancing redox reactions

Here are the steps for balancing redox reactions using the oxidation state method (also known as the half-equation method):

1. Identify the pair of elements undergoing oxidation and reduction by checking oxidation states
2. Write two ionic half-equations (one of the oxidation, one for the reduction)
3. Balance elements and then charges by adding electrons
4. Multiply one or both half-equations so they contain equal numbers of electrons
5. Add the two half-equations and cancel like terms

Worked example 1

We will use a metal displacement reaction to explain how balancing redox reactions using the oxidation state methods works.

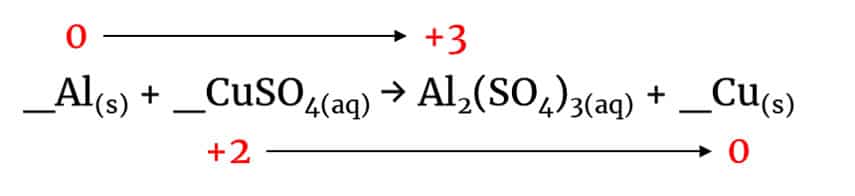
_Al_(s) + _CuSO_4(aq) → Al₂(SO₄)_3(aq) + _Cu_(s)

Step 1: Identify the pair of elements undergoing oxidation and reduction by checking oxidation states

Aluminium is in the form of the element on the LHS and a compound on the RHS, so its oxidation state must have changed (remember, the oxidation state of elements is zero).

Since SO₄^2- ions have a -2 charge and there are 3 of them giving +6 in total, it means each of the 2 Al ions on the RHS must have a +3 charge. This would make sense, since it’s a Group III element so has three valence electrons.

Copper has also changed oxidation state from +2 on the LHS (we know this because it is paired up with one SO₄^2- ion in CuSO₄) to 0 on the RHS.

Step 2: Write two ionic half-equations (one of the oxidation, one for the reduction)

We can now write two ionic half-equations to reflect the oxidation state changes. If you’re not sure how to write ionic equations and ionic half-equations, check out my other post here.

Remember that ionic equations only show the ions participating in the reaction and don’t show spectator ions (handy rule about ionisation: if a substance has the state symbol aq, meaning it’s aqueous or dissolved in water, 99% of the time it will something you can ionise).

Al_(s) → Al³⁺_(aq)

Cu²⁺_(aq)  → Cu_(s)

Step 3: Balance elements and then charges by adding electrons

The elements are already balanced but the half-equations need to be balanced in terms of charge by adding electrons.

We figured out that in the reaction, Al increased oxidation state from 0 to +3. An increase in oxidation state means this is the oxidation reaction:, and since oxidation is loss, the electrons go on the RHS to give the following oxidation half-equation:

oxidation half-equation: Al_(s) → Al³⁺_(aq) + 3e^–

(If we got this wrong and put the electrons on the LHS, the charges would not balance. It would also be odd to see a metal gaining electrons – this is not something you are every likely to see. Metals – particularly reactive metals – typically lose electrons when they react to form cations, making them good reducing agents).

That means copper(II) ions must be undergoing reduction; we figured out that copper changes from +2 to 0, which is a decrease in its oxidation state. The reduction half-equation is:

reduction half-equation: Cu²⁺_(aq) + 2e^– → Cu_(s)

Step 4: Multiply one or both half-equations so they contain equal numbers of electrons

The idea behind this is that as we stated earlier, the number of electrons lost in the oxidation reaction = the number of electrons gained in the reduction reaction. At present, we have aluminium losing three electrons but copper gaining only two. That would mean a redox process that generates a spare electron that never gets used, which would violate the law of Conservation of Matter.

To fix this, we multiply the oxidation half-equation by 2 and the reduction half-equation by 3:

oxidation half-equation: 2Al_(s) → 2Al³⁺_(aq) + 6e^–

reduction half-equation: 3Cu²⁺_(aq) + 6e^– → 3Cu_(s)

Step 5: Combine the two half-equations and cancel like terms

We can now add the two half-equations together:

2Al_(s) +3Cu²⁺_(aq) + 6e^–  → 2Al³⁺_(aq) + 6e^– + 3Cu_(s)

We have to cancel like terms (i.e. terms appearing on both sides of the equation) in chemical equations, which means cancelling the electrons:

2Al_(s) +3Cu²⁺_(aq) + 6e^–  → 2Al³⁺_(aq) + 6e^– + 3Cu_(s)

This gives the balanced redox reaction:

2Al_(s) +3Cu²⁺_(aq)  → 2Al³⁺_(aq) + 3Cu_(s)

If we want the full equation, not just the ionic equation, we just add back the spectator ions and combine them with their metal ions:

2Al_(s) + 3CuSO_4(aq) → Al₂(SO₄)_3(aq) + 3Cu_(s)

Note that we could have saved ourselves a lot of hassle here and just used the subscript rule mentioned in my other post, but this was for illustration purposes.

Balancing redox reactions in acidic solution

If you need to balance a redox reaction that was carried out in acidic solution, use the following set of rules instead:

1. Identify the pair of elements undergoing oxidation and reduction by checking oxidation states
2. Write two ionic half-equations (one for the oxidation, one for the reduction)
3. Balance elements other than O and H, then balance charges by adding electrons
4. Add H₂O to balance oxygen
5. Add H⁺ ions to balance hydrogen
6. Multiply one or both half-equations so they contain equal numbers of electrons
7. Combine the two half-equations and cancel like terms

This seems very complicated I know, but gets easier if you work through a few examples by yourself.

The example we’ll use to illustrate balancing in acidic solution is this one, which appeared on an A Level chemistry paper and caught out a lot of students:

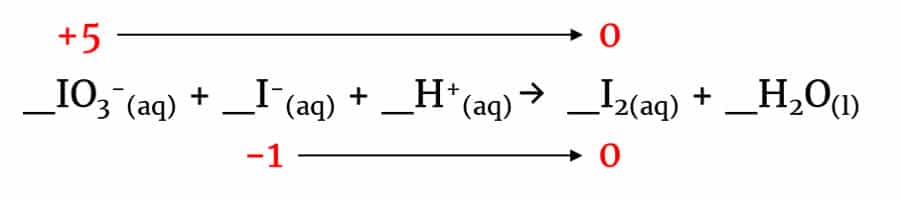
_IO₃^–_(aq) + _I^–_(aq) + _H⁺_(aq) →  _I_2(aq) + _H₂O_(l)

Can you guess what a number of students wrote as the answer? Yep, this:

IO₃^–_(aq) + I^–_(aq) + 6H⁺_(aq) →  I_2(aq) + 3H₂O_(l)

Unfortunately that’s an example of balancing by element but forgetting that charges must also balance. That has a net charge of -4 on the LHS but zero charge on the RHS. Let’s see how it should be balanced.

Step 1: Identify the pair of elements undergoing oxidation and reduction by checking oxidation states

Checking the oxidation states of the elements in this redox reaction reveals that iodine is simultaneously undergoing oxidation and reduction. This is an example of a disproportionation reaction.

Step 2: Write two ionic half-equations (one of the oxidation, one for the reduction)

Iodine is in oxidation state +5 in the iodate(V) ion and changes to 0 in the element. This is the reduction reaction:

IO₃^–_(aq) → 1/2 I_2(aq)

In iodide, it is in oxidation state -1 and also changes to 0 in the element, so this is the oxidation:

I^–_(aq) → 1/2 I_2(aq)

Step 3: Balance elements other than O and H, then balance charges by adding electrons

Iodine’s oxidation state is reduced by 5, so we have to add 5 electrons to the LHS:

5e^– + IO₃^–_(aq) → 1/2 I_2(aq)

In this disproportionation reaction, iodide is also oxidised, losing 1 electron, which we add to the RHS:

I^–_(aq) → 1/2 I_2(aq) + e^–

Step 4: Add H₂O to balance oxygen

The reduction half-equation has 3 oxygen atoms on the LHS and none on the RHS, so we add 3 H₂O molecules to the RHS to correct this:

5e^– + IO₃^–_(aq) → 1/2 I_2(aq) + 3H₂O_(l)

Step 5: Balance H⁺ ions to balance hydrogen

Adding water to correct the oxygen imbalance has obviously added hydrogen atoms. To correct this imbalance, we add protons to the LHS:

6H⁺_(aq) + 5e^– + IO₃^–_(aq) → 1/2 I_2(aq) + 3H₂O_(l)

Step 6: Multiply one or both half-equations so they contain equal numbers of electrons

The reduction half-equation involves 5 electrons but the oxidation half-equation only involves 1.

reduction half-equation: 6H⁺_(aq) + 5e^– + IO₃^–_(aq) → 1/2 I_2(aq) + 3H₂O_(l)

oxidation half-equation: I^–_(aq) → 1/2 I_2(aq) + e^–

Before we can combine them, we need to multiply the oxidation half-equation by 5:

reduction half-equation: 6H⁺_(aq) + 5e^– + IO₃^–_(aq) → 1/2 I_2(aq) + 3H₂O_(l)

oxidation half-equation: 5I^–_(aq) → 5/2 I_2(aq) + 5e^–

(If you think this looks absolutely horrendous with all these fractions, worry not, it will all sort itself out in the end!)

Step 7: Add the two half-equations and cancel like terms

Add the two half-equations together, combine the fractions and cancel the electrons:

6H⁺_(aq) + 5e^– + IO₃^–_(aq) + 5I^–_(aq) → 1/2 I_2(aq) + 3H₂O_(l) + 5/2 I_2(aq) + 5e^–

6H⁺_(aq) + IO₃^–_(aq) + 5I^–_(aq) → 3I_2(aq) + 3H₂O_(l)

This is now balanced.

Balancing redox reactions in basic solution

If the redox reaction was carried out in basic solution (i.e. alkaline conditions), then we have to put in an extra step to balance the equation.

The steps for balancing redox reactions in basic solution are:

1. Identify the pair of elements undergoing oxidation and reduction by checking oxidation states
2. Write two ionic half-equations (one for the oxidation, one for the reduction)
3. Balance elements other than O and H, then balance charges by adding electrons
4. Add H₂O to balance oxygen
5. Add H⁺ ions to balance hydrogen
6. Multiply one or both half-equations so they contain equal numbers of electrons
7. Add OH^– ions equal to the number of H⁺ ions to both sides
8. Add the two half-equations, combine H⁺ and OH^– to form H₂O, then cancel like terms

The example we’ll use is another disproportionation reaction, this time between chlorine and sodium hydroxide:

_Cl_2(aq) + _NaOH_(aq) → _NaCl_(aq) + _NaClO_(aq) + _H₂O_(l)

Step 1: Identify the pair of elements undergoing oxidation and reduction by checking oxidation states

In this reaction, chlorine disproportionates forming chlorate(I) and chloride:

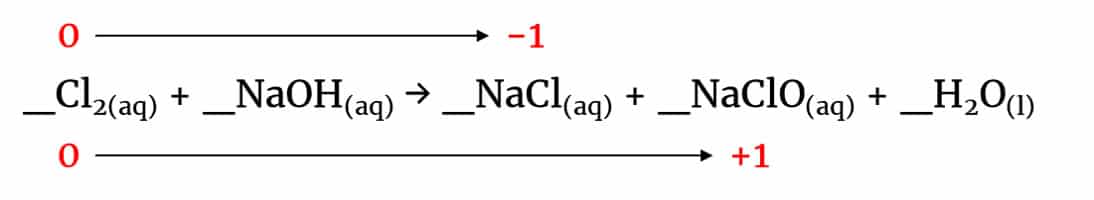
Step 2: Write two ionic half-equations (one of the oxidation, one for the reduction)

We can lose Na⁺ since it’s just a spectator, which gives the following pair of ionic half-equations:

1/2 Cl_2(aq) → Cl^–_(aq)

1/2 Cl_2(aq) → ClO^–_(aq)

Step 3: Balance elements other than O and H, then balance charges by adding electrons

Not much to do at this point other than add in electrons. Remember, they go on the LHS for the reduction half-equation (reduction is gain) and the RHS for the oxidation half-equation (oxidation is loss):

reduction half-equation: e^– + 1/2 Cl_2(aq) → Cl^–_(aq)

oxidation half-equation: 1/2 Cl_2(aq) → ClO^–_(aq) + e^–

Step 4: Add H₂O to balance oxygen

This stage and the next are identical to what is done for balancing redox equations in acidic solution. First, correct the oxygen imbalance by adding water:

e^– + 1/2 Cl_2(aq) → Cl^–_(aq)

H₂O_(l) + 1/2 Cl_2(aq) → ClO^–_(aq) + e^–

Step 5: Add H⁺ ions to balance hydrogen

Then correct the hydrogen imbalance that was created by adding water using H⁺ ions:

e^– + 1/2 Cl_2(aq) → Cl^–_(aq)

H₂O_(l) + 1/2 Cl_2(aq) → ClO^–_(aq) + e^– + 2H⁺_(aq)

Step 6: Multiply one or both half-equations so they contain equal numbers of electrons

Both equations already contain the same number of electrons, so nothing to do at this point.

Step 7: Add OH^– ions equal to the number of H⁺ ions to both sides

This step is different. Since we are in basic solution, any H⁺ ions present would have combined with OH^– to create water. To each half-equation that contains H⁺ ions, we add the same number of OH^– ions to both sides of the equation to consume the H⁺ ions:

In this case, that means adding 2 OH^– ions to both sides of the oxidation half-equation:

e^– + 1/2 Cl_2(aq) → Cl^–_(aq)

2OH^–_(aq) + H₂O_(l) + 1/2 Cl_2(aq) → ClO^–_(aq) + e^– + 2H⁺_(aq) + 2OH^–_(aq)

Step 8: Add the two half-equations, combining H⁺ and OH^– to form H₂O, then cancel like terms

First just add the half-equations together:

e^– + Cl_2(aq) + 2OH^–_(aq) + H₂O_(l)  → ClO^–_(aq) + e^– + 2H⁺_(aq) + 2OH^–_(aq) + Cl^–_(aq)

Combine H⁺ and OH^– to make water:

e^– + Cl_2(aq) + 2OH^–_(aq) + H₂O_(l)  → ClO^–_(aq) + e^– + 2H₂O_(l) + Cl^–_(aq)

Cancel like terms:

e^– + Cl_2(aq) + 2OH^–_(aq) + H₂O_(l)  → ClO^–_(aq) +  e^– + 2H₂O_(l) + Cl^–_(aq)

Adding back the spectator ions gives the balanced equation:

Cl_2(aq) + 2NaOH_(aq)  → NaClO_(aq) +  H₂O_(l) + NaCl_(aq)