
Chemistry calculations: limiting and excess reactants in chemistry
The mole has been baffling chemistry students since it was conceived in the nineteenth century so it’s little wonder that the applied concept of limiting reactants confuses students of all levels. Here are three methods to help you get to grips with limiting reactant calculations.
But first, pancakes.
I bet at some point when you were first being taught about moles, to help you get your head around the idea, your teacher said “the mole is just a number of things, the same way a dozen is twelve of something”.
Everyday analogies can help understand some of the weird, abstract ideas you meet in chemistry. Here’s a situation that you might encounter in the kitchen.
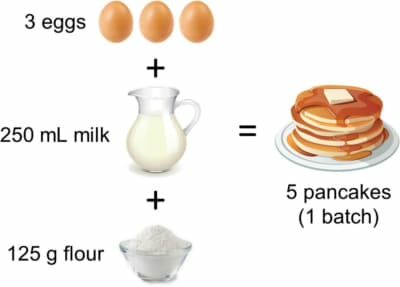
Suppose it’s pancake day and you’re having friends over, so you look up the following recipe on the internet:
5 pancakes aren’t really a lot though you think – what is everyone else going to eat?!
You need to make more than 5, so you check what ingredients you have in the cupboard, and find you have:
The question is, how many pancakes can you make with this lot?
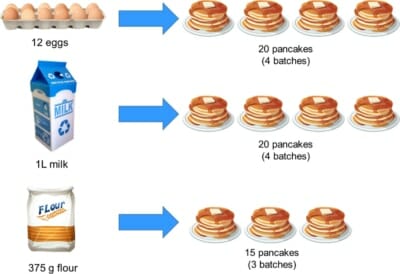
If 3 eggs make 5 pancakes, then with 12 eggs we can make 12/3 x 5 = 20 pancakes. So, we can make four batches, right?
Well that’s true in theory, but there’s a caveat: we can only make four times as many if we have enough of the other ingredients.
How do we check if that’s the case? Easy, just scale up the quantities for the other ingredients by the same factor to see how much of each we’d need, then compare with what we have. Here, the factor we’re scaling up by is 4.
First let’s check if we have enough milk. We needed 250 mL for the recipe with 3 eggs, so if we’re going to use all 12 eggs, we’ll need 12/3 x 250 mL = 1,000 mL of milk. That’s one litre of milk, which is what we have.
Now the flour. The recipe needs 125 g to make one batch, but we’re scaling everything up by a factor of 4. We therefore would need 4 x 125 g = 500 g but uh-oh, we only have 375 g!
There isn’t enough flour to use up all our eggs and milk, so we can’t make 20 pancakes after all.
To work out how many pancakes we could make, we take the total amount of flour we have and divide it by the amount needed to make one batch. 375 / 125 = 3, which tells us we can only make 3 batches, or 15 pancakes. Sad day 🙁
So, what does this tell us?
To make these 15 pancakes, we scaled up the original recipe by a factor of 3 and used 3 x 3 = 9 eggs (leaving 3 leftover) and 3 x 250 = 750 mL of milk (leaving 250 mL leftover).
You could describe the flour in this scenario as the limiting ingredient and the eggs and milk as the excess ingredients.
Some important things to note here:
- The limiting ingredient limits the total amount of pancakes we can make
- The limiting ingredient is the one used to calculate how many pancakes we can make
- The limiting ingredient is also the one used to calculate how many ingredients we’ll have leftover
Why is limiting reactants a thing in chemistry?
Recipes require specific quantities and ratios, but we buy ingredients in all sorts of package sizes. It’s no surprise to find that for some recipes, we’ll have too few of some ingredients and too many of others.
A chemical equation is also really a recipe where the quantities are in moles. It says X moles of this react with Y moles of that to give Z moles of this. We follow the recipe, calculate masses and volumes required, and mix the reactants together.
Why would we need to worry about one reactant limiting the amount of product? Is this just a concept dreamed up to torture chemistry students?
Actually, no. There are several reasons why we’d deliberately not mix reactants in the proportions suggested by the chemical equation. These include:
- To ensure the reaction goes to completion (meaning that the reaction has finished because the reactants are used up). Let’s say we wanted to work out how much calcium carbonate is present in eggshell. We can react the eggshell with excess acid, then titrate the acid remaining with an alkali to work out how much acid was used. Using an excess of acid guarantees all the calcium carbonate in the eggshell reacts. If we don’t ensure this, our analysis will be inaccurate
- The reaction may reach equilibrium and we want to use excess reactants to maximise the amount of product formed
- One of the reactants may be impure, so we use extra to compensate for impurities and ensure we have enough to fully react
- One of the reactants may be unstable, so we use an additional amount of it to compensate for any that might decompose during the reaction
The Golden Rule
If you find limiting reactant calculations confusing and your head is just a fog of numbers when working through them, remember the golden rule:
“The limiting reactant is the one used to calculate how much product and leftover reactants will be present at the end of the reaction”
Once you’ve found the limiting reactant, just focus on it because in 99% of questions you’ll use it as the basis for calculating everything you need to know.
The Methods
There is no ‘official’ way of doing limiting reactant calculations, so think of these methods as training methods to help you structure the calculations until you get used to them. At that point you’ll be able to take shortcuts to arrive at the solutions must faster.
The method I usually teach first is a step-by-step approach where you use the chemical equation to generate ‘rules’ that state how much of each reactant is theoretically needed based on actual amounts. This method is lengthy but methodical, so it’s helpful if you’re just getting used to the concept of limiting reactants.
The second method will be familiar to students who have studied chemical equilibria and carried out calculations using ICE tables. This method is useful because numbers are organised into a table. This method also makes it easy to quickly calculate the amounts of all substances at the end of the reaction.
Finally, there is a variation of the ICE table method that is applicable for gaseous reactions. This can be useful in multiple choice questions on limiting reactants where you need to find the answer quickly without too much calculation.
Method 1: Stepwise approach
Iron reacts with sulfur as shown in the following equation:
Fe(s) + S(s) → FeS(s)
168 g of iron is reacted with 64 g of sulfur. How many grams of iron sulfide are formed?
1. Convert masses into moles using moles = mass / Mr
Mol of Fe = 168 / 56 = 3 mol
Mol of S = 64 / 32 = 2 mol
2. Write a rule for the reactant mole ratios (“X moles of A reacts with Y moles of B…”)
1 mol of Fe reacts with 1 mol S
Mol of Fe = mol of S
3. Using the rule, work out how many moles of each reactant is required
Mol of Fe required = mol of S = 2 mol
Mol of S required = mol of Fe = 3 mol
4. Compare required and actual moles to find limiting and excess reactants
Mol of Fe required = 2 mol, we have 3 mol hence Fe is the excess reactant
Mol of S required = 3 mol, we have 2 mol hence S is the limiting reactant
5. Write a rule for the limiting reactant and product ratios
1 mol S produces 1 mol FeS
Mol of S = mol of FeS
6. Using the limiting reactant rule, work out how many moles of product are formed
2 mol of S produces 2 mol of FeS
7. Convert moles into masses using mass = Mr x moles
Mr(FeS) = 88 g
Mass of FeS produced = 2 x 88 = 176 g
Alternative approach to finding the limiting reactant
You can also find the limiting reactant by calculating how much product would be formed from each of your reactants. The limiting reactant will be the one that gives the least amount of product.
In the above example, 3 moles of Fe would give 3 moles of FeS, which would have a mass of 264 g
2 moles of S would give 2 moles of FeS, which would have a mass of 176 g . From this we can tell that S is limiting.
Method 2: Use an ICE table
260 g of iron(III) oxide are reacted with 96 dm3 of hydrogen gas.
Fe2O3(s) + 3H2(g) → 2Fe(s) + 3H2O(l)
Calculate the mass of iron produced from the reaction. 1 mol of gas occupies 24 dm3.
1. Convert masses/volumes into moles
Moles of iron(III) oxide = 260/159.69 = 1.63 mol
Moles of hydrogen = 96/24 = 4 mol
2. Construct an ICE table and fill in the initial moles
In our ICE table, I = initial moles, C = change in moles in terms of x, E = end moles
Mol Fe2O3 = 260/159.69 = 1.63 mol
Mol H2 = 96/24 = 4 mol
Here’s how the ICE table looks to begin with:
| Fe2O3 | 3H2 | 2Fe | 3H2O | |
|---|---|---|---|---|
| Initial moles / mol | 1.63 | 4 | 0 | 0 |
| Change in moles / mol | -x | -3x | +2x | +3x |
| End moles / mol | ? | ? | ? | ? |
Initial moles of products will be zero since none will have formed right at the start of the reaction.
To help understand how the change row is completed, think of x as the amount in moles that reactants change by between the start and end of the reaction. For reactants, x will be negative since their amounts decrease, whilst for products, x is positive as they are being formed.
The coefficients for x come directly from the chemical equation. In this reaction, for every 1 mol of iron(III) oxide and 3 mol of hydrogen that react, we form 2 mol of iron and 3 mol of water.
3. Find the limiting reactant and set its value at the end to zero in the table
Here, 1.63 mol of iron(III) oxide requires 3 x 1.63 mol = 4.89 mol of hydrogen
We have only 4 mol, hence hydrogen is the limiting reactant.
We therefore put a zero under hydrogen in the end row of the ICE table. The column for hydrogen gives a simple equation that says
4 – 3x = 0
Solving this gives x = 1.33 mol
| Fe2O3 | 3H2 | 2Fe | 3H2O | |
|---|---|---|---|---|
| Initial moles / mol | 1.63 | 4 | 0 | 0 |
| Change in moles / mol | -x | -3x | +2x | +3x |
| End moles / mol | ? | 0 | ? | ? |
4. Calculate the moles remaining at the end of the reaction
Using this value of x, we can complete the last row of the table to show what we’d have at the end of the reaction:
| Fe2O3 | 3H2 | 2Fe | 3H2O | |
|---|---|---|---|---|
| Initial moles / mol | 1.63 | 4 | 0 | 0 |
| Change in moles / mol | -x | -3x | +2x | +3x |
| End moles / mol | 0.297 | 0 | 2.67 | 4 |
5. Convert moles into grams or volumes as needed
We can now answer the question.
Mol of iron produced = 2.67 x 55.85 = 149.1 g
If you want to, you can add another row to the table and calculate all the end masses:
| Fe2O3 | 3H2 | 2Fe | 3H2O | |
|---|---|---|---|---|
| Initial moles / mol | 1.63 | 4 | 0 | 0 |
| Change in moles / mol | -x | -3x | +2x | +3x |
| End moles / mol | 0.297 | 0 | 2.67 | 4 |
| End masses / g | 47.4 | 0 | 149.1 | 72.1 |
Method 3: Use gas laws
1.5 dm3 of propane is reacted with 10 dm3 of oxygen. Calculate the total volume of gases formed at the end of the reaction.
C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(g)
When faced with a question on gaseous reactions where you’re given volumes of reactants, you can use Avogadro’s Law, which states
Equal volumes of gas contain equal numbers of molecules when pressure and temperature are constant.
This direct proportionality between moles and volumes means you can use volume directly in the calculation, giving a shorter way to deal with limiting reactant calculations involving gases.
The method for this is as follows:
1. Construct an ICE table (I = initial volume, C = change in volume, E = end volume)
| C3H8 | 5O2 | 3CO2 | 4H2O | |
|---|---|---|---|---|
| Initial volume/ dm3 | 1.5 | 10 | 0 | 0 |
| Change in volume / dm3 | -x | -5x | +3x | +4x |
| End volume / dm3 | ? | ? | ? | ? |
2. Find the limiting reactant and set its value at the end to zero in the table
1.5 dm3 of propane reacts with 5 x 1.5 dm3 = 7.5 dm3 of oxygen
We have 10 dm3 of oxygen, hence oxygen is in excess and propane is limiting. Put a zero in the table under propane:
| C3H8 | 5O2 | 3CO2 | 4H2O | |
|---|---|---|---|---|
| Initial volume/ dm3 | 1.5 | 10 | 0 | 0 |
| Change in volume / dm3 | -x | -5x | +3x | +4x |
| End volume / dm3 | 0 | ? | ? | ? |
3. Calculate the volumes remaining at the end of the reaction
Here, 10 – 5x = 2.5 hence x = 1.5 dm3
With this value, we can complete the ICE table:
| C3H8 | 5O2 | 3CO2 | 4H2O | |
|---|---|---|---|---|
| Initial volume/ dm3 | 1.5 | 10 | 0 | 0 |
| Change in volume / dm3 | -x | -5x | +3x | +4x |
| End volume / dm3 | 0 | 2.5 | 4.5 | 6.0 |
The total volume of gases at the end of the reaction is therefore 2.5 + 4.5 + 6.0 = 13.0 dm3
Still confused?
I hope not but if you’re still baffled, try out this PHET simulation that helps to get your head around the limiting reactant concept using meat and cheese sandwiches!
In the coming weeks (or months, since I’m a little snowed under due to the COVID-19 situation) I’ll be adding worksheets so you can try out these methods.







Limiting and excess reactants are important concepts in chemistry calculations that can determine the yield of a chemical reaction. By understanding these principles and applying them to real-world scenarios, students can gain a deeper understanding of the underlying concepts of chemistry. With the help of a knowledgeable tutor, students can master these calculations and excel in their chemistry studies.